Antamasi tiedot ovat melko rajallisia, mutta haluan yrittää selvittää ne. Tapa, jolla näen sen, sekoitat kolme eri käsitettä kysymyksiisi. Työskentelen puoliympyrän läpi elliptisen suuntaan kohti hyperbolista oletusta.
Puoliympyrä
Tämä on GIF keskeisestä lähteestä, joka lähettää aallon homogeenisessa tilassa:
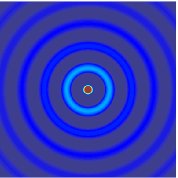
Voit pysäyttää gifin milloin tahansa (vedä sitä hiirellä), ja kaikki aaltoreunat ovat samankeskisiä. Voit myös nähdä tämän, kun tarkastelet aaltoyhtälöä. Ajan muutokset ovat yhtä suuria nopeuden muutosten kanssa avaruudessa. Jos nopeus on vakio, ajanmuutos aiheuttaa samanlaisen muutoksen aallon etenemisessä missä tahansa käytettävissä olevassa suunnassa. Vaikka työskentelemme usein (x, y, z) -koordinaateissa, tässä on helpoin olettaa, että aaltolähteemme on $ (0,0,0) $: ssa ja jos etenemämme on yhtä suuri kaikkiin suuntiin, vektorimme osoittaa nämä avaruuspisteet ovat täydellisen pallon säde.
Jos katsomme puoliavaruutta kuten seismisessä, meillä on puolipallo ja jos skaalaamme takaisin 2D lähdettä ympäröi puoliympyrä. Joten jos kaivamme valtavan määrän pintaa ja sijoitamme vastaanottimia lähteemme ympärille, lähteestä yhtä kaukana olevien tulisi vastata samanaikaisesti lähteen sytyttämisen jälkeen.
Ellipsis
Kuvassa 13 näet puoliympyrän. Tässä kuvassa on useita tärkeitä asioita. Ensimmäinen olisi vastaanotin. Vastaanotin ei ole keskellä, mutta kaikki ne puoliympyrän esimerkissä olevat vastaanottimet ovat myös. Mikä tekee tästä erilaisen, on se, että useiden vastaanottimien sijaan, jotka tallentavat aaltoa samanaikaisesti, tässä on yksi ainoa vastaanotin. Lisäksi ennen kuin lähteemme oli mukava ja keskitetty, nyt se ei ole keskellä.
Valitettavasti tämä ei riitä kuvan 13 ymmärtämiseen. Ensinnäkin, puoliympyrän osalta tarkastelimme suoria aaltoja. Kuvassa 13 näemme heijastuneet aallot. Nyt he ottavat jälleen vakionopeuden, mikä tarkoittaa, että tiheyden muutoksen on selvästi oltava, jotta heijastus tapahtuu. Tämä johtaa meidät yksinkertaisiin teoreettisiin kysymyksiin: "Minulla on mittaus matka-ajalla $ T $. Missä maanpinnan paikoissa tiheysmuutoksen pitäisi olla, jotta selittäisin $ T $: n mittaustani?"
Olet siis rakentamassa tasoa, jossa säteen polku lähteestä kohti tasoa, joka on lisätty säteen polulle tasossa olevasta tapahtumapisteestä vastaanottimeen, on aina pituudeltaan $ T $. Onneksi näin muodostuu puoli-ellipsi.
Voit itse kokeilla tätä merkkijonolla. Ota merkkijono, jonka pituus on $ T $, kiinnitä toinen pää lähdekohtaan, toinen vastaanottimen kohtaan ja laita sitten kynä nostoliinaan ja jäljitä uloin paikka, johon kynällä saatat. Olet luonut pinnan hankinnan alapuolelle, mikä kaikki olisi voinut aiheuttaa vastauksen vastaanottimellasi hetkellä $ T $.
Hauska tosiasia: Jos laitat lähteen ja vastaanottimen takaisin sijaintiin $ x = 0 $, ellipsistasi tulee taas ympyrä. Se ei ole puoliympyrä aikaisemmasta, kuten aiemmin meillä oli suora aalto, nyt katsomme tasavertaisen heijastusmatkan pintaa. Näet tämän seuraavasta kuvasta CC-BY-SA Ag2gaeh:
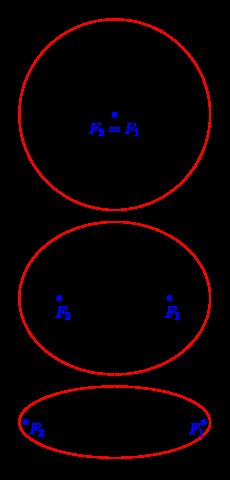
Hyperbola
Kuva 14 vie meidät jälleen askeleen lähemmäksi siirtymistä. Aiemmin katsoit yhtä lähdettä keskeltä ja yhtä vastaanotinta keskeltä. Nyt vaihdamme vaihdetta uudelleen. Katsotaan tässä helpoin tapaus, $ x = 0 $. Tässä lähde ja vastaanotin ovat samassa paikassa, joten matka-aika $ T_0 $ kuvantamispisteeseen I on yhtä pitkä kuin ennen ja jälkeen heijastuksen maanpinnasta. Mutta ennen kuin tiedämme, että tämä paikka voisin olla missä tahansa puoliympyrässä maan alla (mikä olisi ellipsi, ellei se tosiasia, että $ S = R $, kuten näimme aiemmin).
Tarvitsemme siis jotain matematiikan vakuuttamiseksi, että sen sijaan, että sijoittaisimme kuvapisteen I "mihin tahansa puoliympyrään", haluamme tarkan sijainnin. Tässä meillä on useita tapoja tarkastella sitä. Jos pinnan kuvapiste $ I $ on itse asiassa piste, kutsumme sitä diffraktioksi. Diffraktioiden erityinen ominaisuus on, että ne heijastavat aina aaltoasi takaisin sinua kohti (ne hajottavat aallon, joten ne hajottavat aallon kaikkiin suuntiin, siis myös takaisin sinulle). Joten jos sijoitat lähteen ja vastaanottimen sijaintiin x = 1 tässä kuvassa, voimme rakentaa kolmion pisteiden $ I $, $ x = 0 $ ja $ x = 1 $ välille. Tämä tarkoittaa, että matka-aika T_1 voidaan laskea hyvällä ol 'Pythagorasilla ($ a ^ 2 + b ^ 2 = c ^ 2 $): $$ 1 ^ 2 + (T_0 / 2) ^ 2 = (T_1 / 2) ^ 2, $$ ja voimme tehdä tämän jokaisesta pisteestä niin, että: $$ T_N = 2 * \ sqrt (N ^ 2 + T_0 ^ 2/4) $$ ja sitten: $$ T_N = T_0 * \ sqrt ((2N / T_0 ) ^ 2 + 1) $$ Tämä kuvaa sattumalta hyperbolan epäkeskisyyttä. Tämä on yksi tapa etsiä diffraktiohyperboleja, on olemassa useita muita, mutta yritin pitää kiinni annetuista luvuista.